Pre:

查了一些有关uniswap源码解析的文章，找到这篇Uniswap 解析：恆定乘積做市商模型 Constant Product Market Maker Model 的 Vyper 實作里面讲得非常清楚，涉及到一些数学公式的推导，自己推导一遍，之后再去看uniswap的代码会清晰很多。

恒定乘积公式

无手续费:

x * y = k

令交易的两虚拟货币为 X 和 Y，各自数量为 x 和 y
两货币数量的乘积 x * y 恆等于 k
k 值是由第一笔注入的流动性所决定

因此，用∆x数量的X币来购买Y币所能得到的数量∆y、或是为了购买∆y需要付出的∆x数量

依照此公式进行计算：(x+∆x)(y-∆y) = k，而交易的价格就是两币量 ∆x 和 ∆y 的比。

以下公式用 α = ∆x / x 和 β = ∆y / y 来表示 ∆x 和 ∆y 及 X Y 两币在交易发生后的新均衡数量：

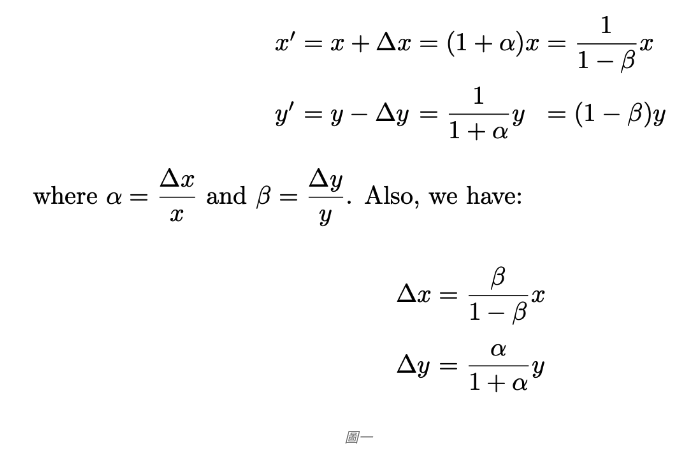
公式推导:

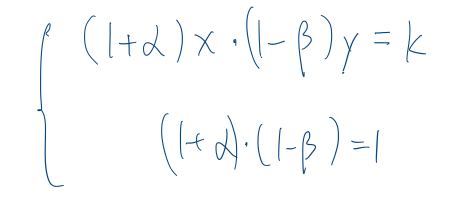
这样可以推导出前2行

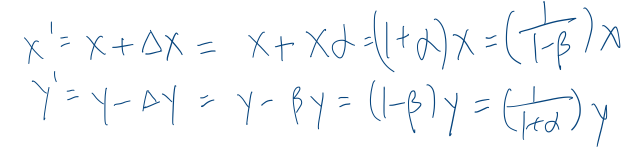
接着推导∆x

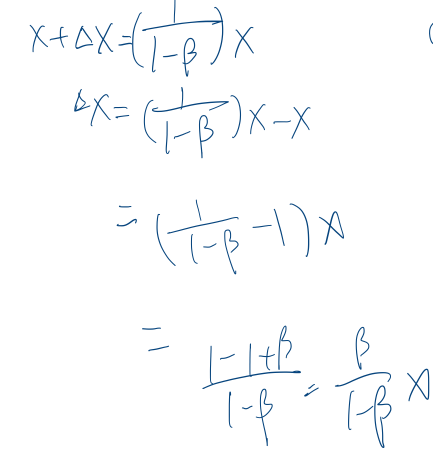
推导∆y

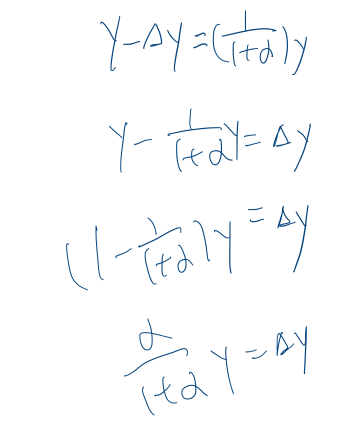
第一个图里的公式，都推导完了。

计入手续费:

在 Uniswap 进行的每一笔交易都会被收取 ρ = 0.003 / 0.3% 的手续费回馈给流动性提供者liquidity provider，因此要将手续费纳入公式的考量：

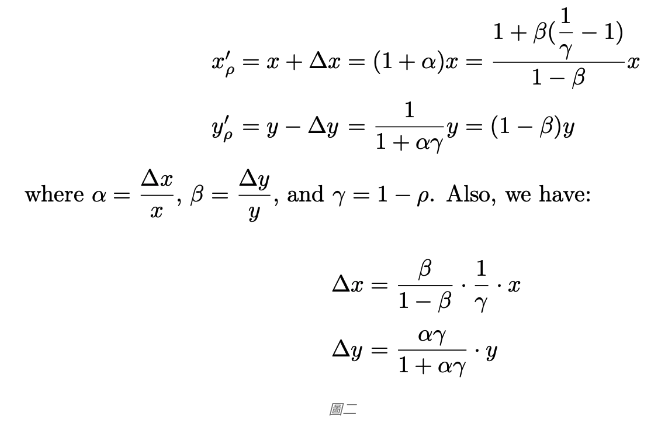
文里作者推荐从 ∆x 和 ∆y 两值开始去推导

手续费 ρ = 0.3% 的意思是会从付款中扣掉 0.3 %，也就是从∆x扣。

在有手续费的情况下 ∆x 就变成了 (1-ρ)∆x ，若令 γ = 1-ρ 则为 γ∆x。因此，将图一中的 ∆x 换成 γ∆x，就会得到以下式子：

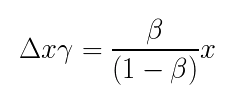
将等号左方的 γ 移到右方后就得到了图二中的 ∆x

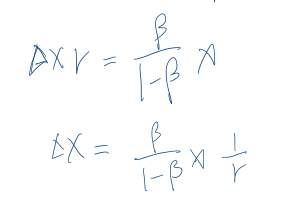
接着推导∆y

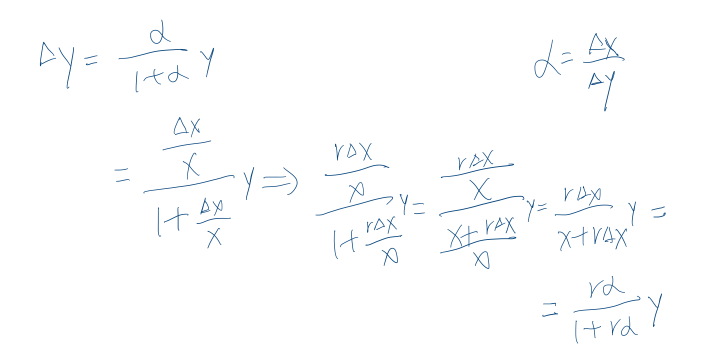
而 x’ 还有 y’ 就可以由 ∆x 和 ∆y 推出来

推导x’ ：

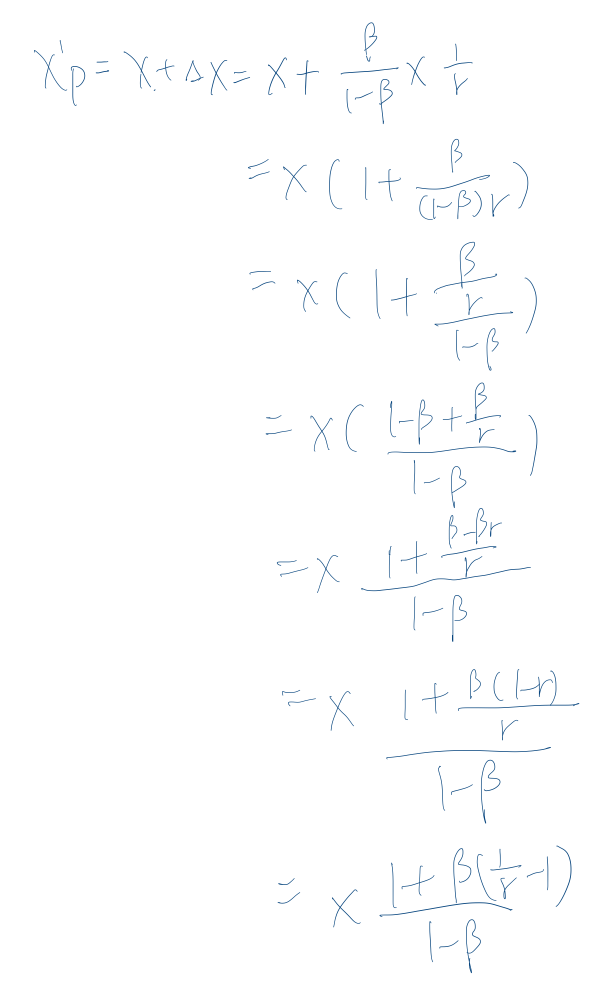
推导y’ ：

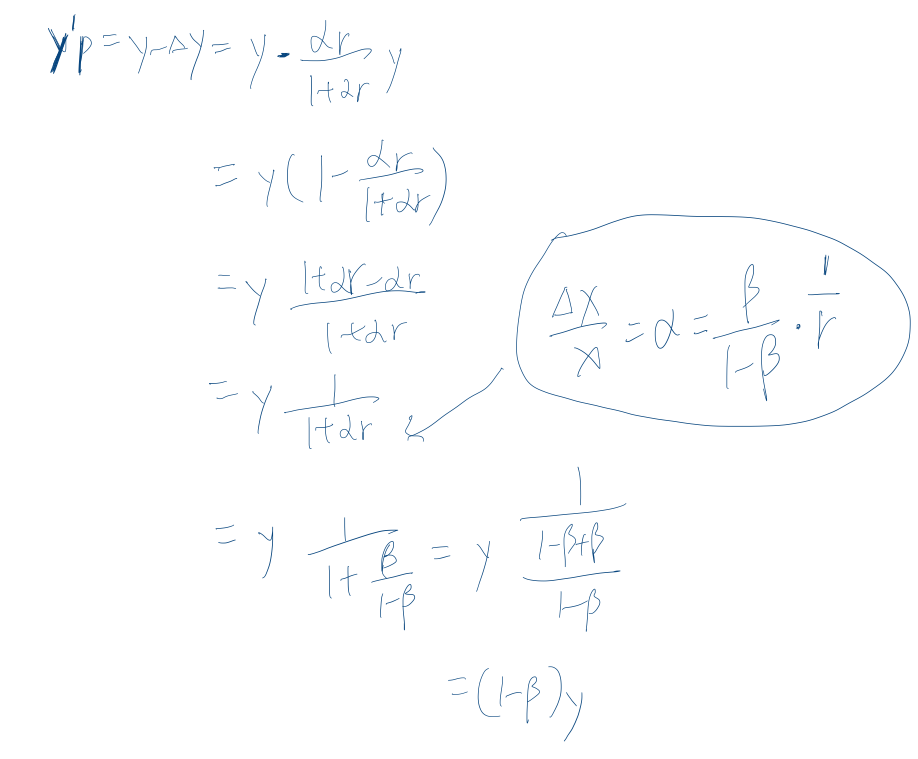
将图二中得到的 x’ 和 y’ 相乘，会得到：

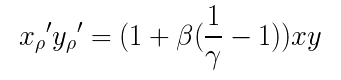
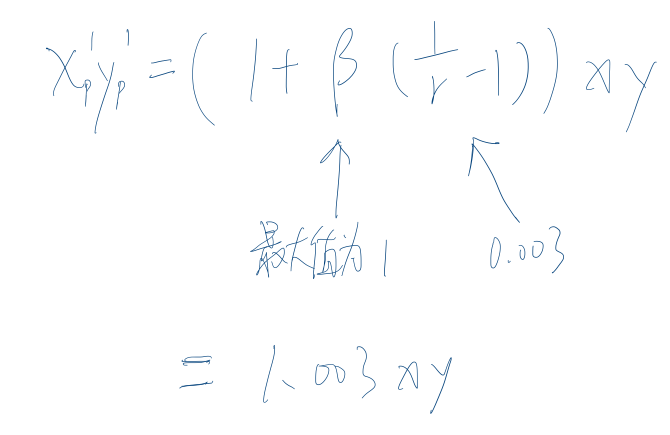
当有手续费使得γ != 1或ρ != 0，x’ρ * y’ρ 的值其实会稍微和 xy = k 不同

实际上 γ = 0.997 或 ρ = 0.003，因此 1除以0.997-1 => 1/γ-1 ≒ 0.003。

β = ∆y / y 代表的是换得的 Y 币佔总量的比例，即使最大值为1(全部兑换出来)，误差也只有 1 * 0.003，故可知手续费 = 0.3% 对于 k 值的影响极小。

相关代码:

给定∆x能购买多少∆y

// @dev 获取的单个输出数额
// @notice 给定一项资产的输入量和配对的储备，返回另一项资产的最大输出量
// @param amountIn 输入数额
// @param reserveIn 储备量In
// @param reserveOut 储备量Out
// @return amountOut 输出数额
// given an input amount of an asset and pair reserves, returns the maximum output amount of the other asset
function getAmountOut(uint amountIn, uint reserveIn, uint reserveOut) internal pure returns (uint amountOut) {
	// 确认输入数额大于0
	require(amountIn > 0, 'UniswapV2Library: INSUFFICIENT_INPUT_AMOUNT');
	// 确认储备量In和储备量Out大于0
	require(reserveIn > 0 && reserveOut > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY');
	// 税后输入数额 = 输入数额 * 997
	uint amountInWithFee = amountIn.mul(997);
	// 分子 = 税后输入数额 * 储备量Out
	uint numerator = amountInWithFee.mul(reserveOut);
	// 分母 = 储备量In * 1000 + 税后输入数额
	uint denominator = reserveIn.mul(1000).add(amountInWithFee);
	// 输出数额 = 分子 / 分母
	amountOut = numerator / denominator;
}

上面已知

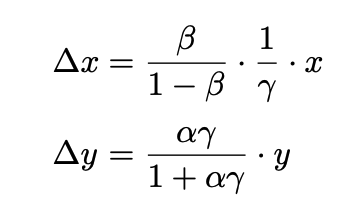
代码和公式表达方式不同，因此先将 α = ∆x / x 和 β = ∆y / y 代换回来并将上下同乘 x：

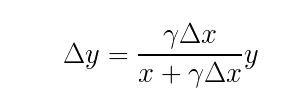
由于 γ = 0.997，可以将上下同乘 1000 后得到：

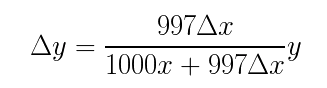
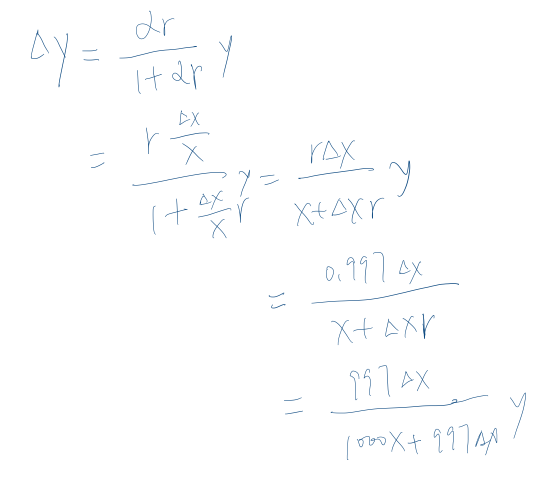
将代码和公式结合起来：

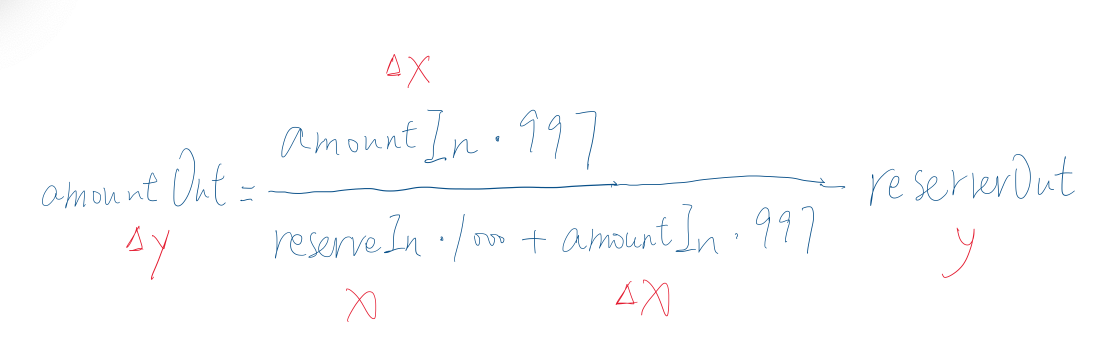
getAmountOut函数，通过入参：

amountIn —— ∆x —— ∆x数量的x币
reserveIn —— x —— x币的储备量/池子原有的x币数量
reserveOut —— y —— y币的储备量

计算出参:

amountOut —— ∆y —— ∆y数量的y币

指定的∆y需要多少∆x

// @dev 获取的单个输入数额
// @notice 给定一项资产的输出量和配对的储备，返回其他资产的所需输入量
// @param amountOut 输出数额
// @param reserveIn 储备量In
// @param reserveOut 储备量Out
// @return amountIn 输入数额
// given an output amount of an asset and pair reserves, returns a required input amount of the other asset
function getAmountIn(uint amountOut, uint reserveIn, uint reserveOut) internal pure returns (uint amountIn) {
	// 确认输出数额大于0
	require(amountOut > 0, 'UniswapV2Library: INSUFFICIENT_OUTPUT_AMOUNT');
	// 确认储备量In和储备量Out大于0
	require(reserveIn > 0 && reserveOut > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY');
	// 分子 = 储备量In * 储备量Out * 1000
	uint numerator = reserveIn.mul(amountOut).mul(1000);
	// 分母 = 储备量Out - 输出数额 * 997
	uint denominator = reserveOut.sub(amountOut).mul(997);
	// 输入数额 = ( 分子 / 分母 ) + 1
	amountIn = (numerator / denominator).add(1);
}

一样先将 α = ∆x / x 、β = ∆y / y 和 γ = 0.997 代换并上下同乘 1000y 得到：

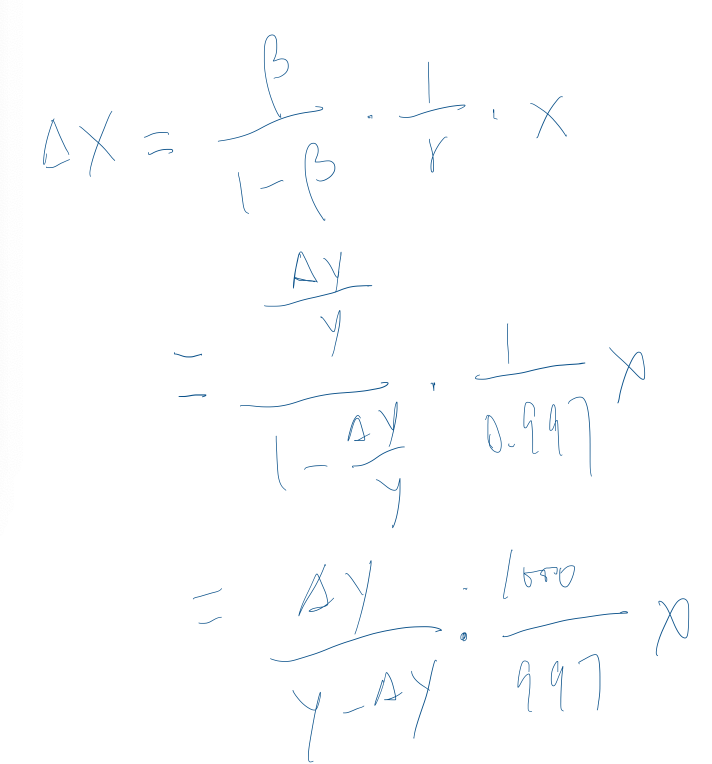
将代码和公式结合起来：

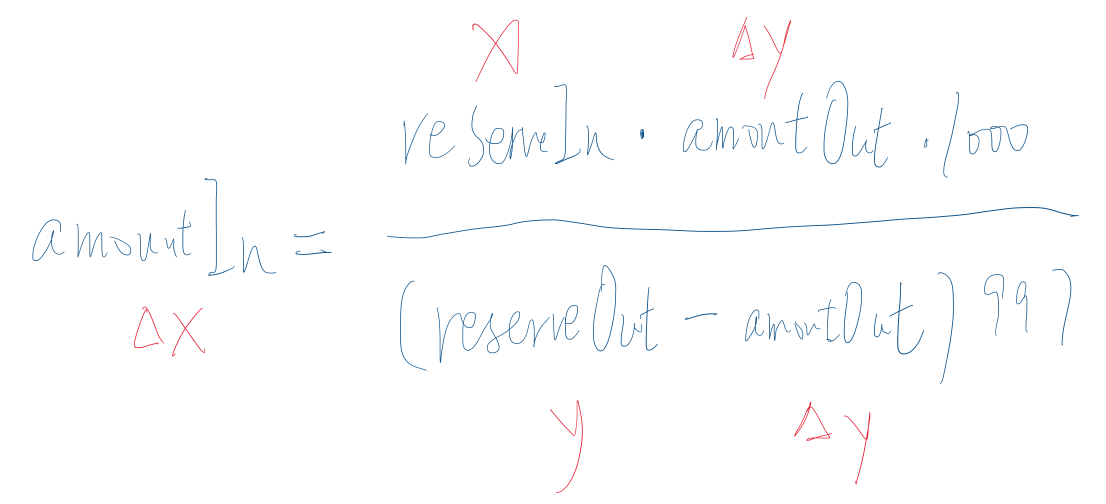
getAmountIn函数，通过入参：

amountOut —— ∆y —— ∆y数量的y币
reserveIn —— x —— x币的储备量/池子原有的x币数量
reserveOut —— y —— y币的储备量

计算出参:

amountIn —— ∆x —— ∆x数量的x币

最后有个+1，因为solidity在进行整数除法的时候，余数部分是会被抛弃掉的，相当于向下取整。
+1之后，交易者需要付出多一点点

Trash Bin

TechNotes-Uniswap-恒定乘积公式原理

Pre:

恒定乘积公式

无手续费:

计入手续费:

相关代码:

Refs: